دوران: (rotation)

دوران به معنی چرخش ، چرخیدن و دور گردیدن می با شد و در ریاضی گرداندن یک شکل حول یک نقطه یا خط را دوران می نامیم .

دوران دو نوع می باشد:

نماد های  دوران مرکزی،

و نمادهای دوران  محوری را نشان می دهند.

مجموعه دوران ها: مجموعه ای از دوران هاست که پس از انجام دوران وضعیت شکل و رنگ آن را حفظ می کنند. گاهی مجموعه دوران ها را مجموعه تقارن ها نیز می نامند.

مجموعه ی را مجموعه ی دوران ها ی شکل بالا می نامیم.

نويسنده : یاسین باژن | تاريخ : چهار شنبه 13 آذر 1391برچسب:,

| نوع مطلب : <-PostCategory-> |

مساحت به معنی اندازه گرفتن زمین، پیمایش زمین، سطح محوطه و زمینی و سطح به معنی رویه، بالای هر چیز که هموار و پهن باشد؛ در اصطلاح هندسه اندازه ی سطح هر شکل هندسی را مساحت می نامیم.  

مساحت شکلهای هندسی:

1) مساحت مربع

3) مساحت متوازی الاضلاع

4) مثلث

6) ذوزنقه

7) دایره

مساحت دایره

اگز یک دایره را به وسیله ی قطرهای آن به 6 قسمت مساوی تقسیم کنیم و با توجه به شکل زیر آنرا ببریم و کنار هم قرار دهیم، مساحت شکل حاصل با مساحت دایره برابر است.

اگر دایره را به 12 قسمت مساوی تقسیم کنیم و قسمتها را کنار هم قرار دهیم شکل زیر بدست می آید.  

اگر دایره ای را به 24 قسمت مساوی تقسیم کنیم و قسمتها را کنار هم قرار دهیم شکل زیر بدست می آید.  

 چنانکه مشاهده می کنید هر قدر تعداد قسمتها زیاد می شود شکل حاصل از کنار هم قرار دادن این قسمتها به یک مستطیل نزدیکتر می شود که مساحت آن با مساحت دایره برابر است. طول این مستطیل با نصف محیط دایره و عرض  آن با شعاع دایره برابر است. پس،

شعاع × نصف محیط دایره = مساحت دایره

اندازه شعاع را باr  ، عدد 14/3 را با p و مساحت دایره را با A نشان دهیم.

بنابراین، مساحت دایره برابر است با حاصلضرب عدد p در مجذور شعاع

نويسنده : یاسین باژن | تاريخ : چهار شنبه 29 آبان 1391برچسب:,

| نوع مطلب : <-PostCategory-> |

معادله خط: (Line   equation) رابطه ی بین طول (X) و عرض (Y) نقاط واقع بر یک خط را معادله ی آن خط می گویند که به صورت یک تساوی نوشته می شود .

مثال: به خط L توجه کنید . نقاط روی این خط قرار دارند .مشاهده می کنیم که طول و عرض این نقاط با هم مساویند . هر نقطه ای که طول و عرض آن مساوی باشد بر خط L قرار می گیرد و هر نقطه ای که روی خط L باشد طول و عرض آن مساوی است.

اگر طول هر نقطه را با X و عرض آن را با Y نشان دهیم ، رابطه Y=X را معادله ی خط (L) می نامیم. این تساوی، رابطه ی بین طول و عرض نقاط را مشخص می کند.

انواع خط:

در هر یک از تصاویر زیر به خط رسم شده توجه کنید .مختصات نقاط داده شده از خط را بیان کنید و معادله ی خط را بنویسید.

 تصویر 1:

 حل:   

نکته: این نوع خط ها موازی محور طول ها هستند و معادله ی آن ها به صورت Y=b نوشته می شود . (b یک عدد ثابت برای همه ی نقاط می باشد.)

مانند   1=Y=-2  ،    y و ........◦

تصویر2:  

حل: 

نکته: این نوع خط ها موازی محور عرض ها هستند و معادله ی آن ها به صورت x=a نوشته می شود. (a یک عدد ثابت برای طول همه ی نقاط می باشد.)

مانند   1=X=-2  ،    X و ........◦

تصویر3: 

حل: 

نکته: این نوع خط از مبدأ مختصات می گذرد و معادله ی آن به صورت  Y=mx نوشته می شود.

مانند:   

 تصویر 4:  

حل: 

نکته: این نوع خط نه موازی محوری است، نه از مبدأ مختصات می گذرد و معادله ی آن به صورت Y=mx+n می با شد. مانند:

دانش آموزان عزیز: انواع دیگری از خط را که به نظرتان می رسد در یک صفحه ی مختصات رسم کنید و در مورد معادله خط مربوط به هر کدام تحقیق کنید.

صورت استاندارد معادله خط:

هر رابطه ی درجه ی اول بین X و Y مانند: 1-Y=2x و 6=3x+Y را معادله ی خط گو یند صورت استاندارد معادله ی خط   Y=mx+n می باشد که در آن m و n دو عدد معلوم و مشخص هستند.صورت دیگر معادله ی خط ax+by=c   می باشد که در آن c و b و a سه عدد معلوم می باشند که با هم صفر نیستند و آنرا معادله ی خطی یا معادله ی ضمنی می نامند.

رسم خطی که معادله ی آن داده شده است:

برای رسم یک خط راست به ترتیب زیر عمل می کنیم .

الف:مختصات دو نقطه ی دلخواه آن خط را پیدا می کنیم .

ب:جای این دو نقطه را درصفحه ی مختصات مشخص می کنیم .

ج: این دو نقطه را به هم وصل کرده از دو طرف امتداد می دهیم.

مثال:در هر یک از تصاویر زیر معادله ی یک خط داده شده است. نمودار هر یک از خط های داده شده را رسم کنید.  

 تصویر 1:      Y=۲x+۵

حل:ابتدا عدد های مختلفی به x می دهیم و عدد های نظیر آن ها را برای y به دست می آوریم.

ادامه مطلب در ادامه مطلب

ادامه مطلب ...
نويسنده : یاسین باژن | تاريخ : چهار شنبه 22 آبان 1391برچسب:,

| نوع مطلب : <-PostCategory-> |

الف: مجموعه عددهای صحیح

عدد صحیح:(integer)

صحیح به معنی تندرست، سالم و درست می باشد و هر یک از اعداد 0 , 1± , 2± , ... را یک عدد صحیح       می نامیم. مجموعه ی اعداد صحیح را با حرف که از کلمه آلمانی Zahlen به معنی «عدد صحیح» گرفته شده است، نمایش می دهند. این مجموعه عبارت است از:

{ ... , 3+ , 2+ , 1+ , 0 , 1- , 2- , 3- , ...} =

نمایش مجموعه عددهای صحیح:

برای معرفی یک مجموعه روشهای مختلفی وجود دارد. اگر اعضای مجموعه مشخص باشند، اعضای مجموعه را می نویسیم مانند: مجموعه کتابهای درسی سال سوم دوره راهنمایی تحصیلی گاهی اوقات لازم است به جای نوشتن اعضای یک مجموعه ، خاصیت اعضاء آن را بیان کنیم. به عنوان مثال فرض کنید معاون پرورشی یک مدرسه خطاب به دانش آموزان آن مدرسه می گوید:

دانش آموزانی که در نوبت اول معدل آن ها بیشتر از 18 باشد ، به اردوی علمی ، تفریحی در شهر اصفهان خواهند رفت. در این جا اعضای مجموعه فعلا مشخص نیستند ، بلکه ویژگی و خاصیت اعضای مجموعه که معدل بالای 18 می باشد در آینده ای نزدیک اعضای مجموعه رامشخص خواهد کرد.

اکنون مجموعه اعداد صحیح بین 3+ و 3- را در نظر بگیرید و به معرفی این مجموعه در حالتهای مختلف توجه کنید:

الف) نمایش مجموعه اعداد صحیح بین 3+ و 3- روی محور اعداد صحیح:

ب) نمایش مجموعه اعداد صحیح بین 3+ و 3- به زبان ریاضی:

ج) نمایش مجموعه اعداد صحیح بین 3+ و 3- با نوشتن اعضای آن مجموعه:

{ 2 , 1 , 0 , 1- , 2- }=A

مثال: مجموعه های زیر با علائم ریاضی بیان شده اند. آن ها را با اعضاء مشخص کنید:

الف):

حل:  مجموعه A بیان می کند : « x بطوریکه x به اعداد صحیح تعلق دارد و مربع آن برابر عدد یک است.» . پس از خواندن این جمله باید اعدادی را که واجد این خاصیت هستند، پیدا کنیم. بدیهی است که عددهای صحیح 1+ و 1- این خاصیت را دارند بنابراین :

{ 1- و 1+} =A

ب):

حل: گاهی اوقات به جای به کاربردن متغیر ، عبارتی جبری شامل متغیر بکار می رود.

(2^x) نماینده اعضای این مجموعه است که بیان می کند x  به اعداد طبیعی تعلق دارد. بنابراین:

{ ... و 16 و 8 و 4 و 2}=B

جمع عددهای صحیح:

الف) جمع با توجه به بردار:

مثال: جمع متناظر با بردار را بنویسید.

حل:

( عدد انتهای بردار) = (طول بردار)+ ( عدد ابتدای بردار)

 ( 3+ )  =     ( 5+ )   +   ( 2- )

ب) جمع بدون توجه به بردار: برای نوشتن حاصل جمعه به صورت زیر عمل می کنیم:

1. ابتدا تا حد امکان مختصر نویسی می کنیم.

2. اگر عددها هم علمت باشند، جمع می کنیم و اگر مختلف العلامت باشند، کم می کنیم.

3. علامت جواب بدست آمده را مشخص می کنیم.

مثال: 7=5-12=(5-)+(12+)

یادآوری: چنانچه بخواهیم از قرینه یابی استفاده کنیم به صورت زیر عمل می کنیم:

11-=(4+7)-=(4-)+(7-)

5-=(10-15)-=(10+)+(15-)

4-=(8-12)-=(12-)+(8+)

تفریق عددهای صحیح:

الف) تفریق با استفاده از بردار:

مثال:  تفریق متناظر با بردار را بنویسید.

حل: (عدد ابتدای بردار) = ( طول بردار) - ( عدد انتهای بردار)

                           ( 3- ) = ( 4+ ) - ( 1+ )

ب) تفریق اعداد صحیح بدون توجه به بردار:

 برای تفریق کردن عدد b از عدد a ، می توانیم قرینه b را با a جمع کنیم: یعنی:

a-b = a+(-b)

مثال:

22=7+15=(7+)+(15+)=(7-)-(15+)

عدد گویا: (rational Number):

گویا صفت فاعلی از مصدر گفتن می باشد و در ریاضی هر عدد کسری مانند یا هر عددی که بتوان آن را به شکل یک کسر نوشت مانند 2- , 0 , 3+ , 2/3- , 25/0 که به ترتیب به شکل کسرهای نوشته می شوند ، را یک عدد گویا می نامیم.

مجموعه عددهای گویا:

 این مجموعه شامل تمام اعداد گویا است، این مجموعه را با حرف Q که حرف اول کلمه Quotient  است، نمایش می دهند.

نمایش مجموعه عددهای گویا به زبان ریاضی به صورت زیر است:

ادامه مطلب در ادامه مطلب

ادامه مطلب ...
نويسنده : یاسین باژن | تاريخ : چهار شنبه 10 آبان 1391برچسب:,

| نوع مطلب : <-PostCategory-> |

یادمه همیشه در مجله های جدول و سرگرمی که تابستونها میخریدم و حل میکردم از قسمت "اختلاف دو تصویر" خوشم میومد.حتماً تابحال دیدین آره؟! دو تاعکس بغل هم که همه چیزشون مثل هم بود مگر بعضی قسمتهای کوچولو که با زرنگی دستکاری شده بود.یادتون اومد؟

حتـــــــــــــماً یادتون اومده

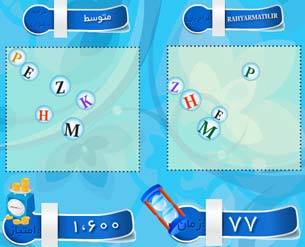
حالا با همین ایده یک بازی براتون ساختم.توی عکس هم میتونید ببینید. در دو قسمت چپ و راست حروف مشابهی قرار گرفته اند ولی در یکی از قسمتها یک حرف کمتره.شما باید اون رو پیدا کنید و با استفاده از صفحه کلید اون رو تایپ کنید و امتیاز بگیرید.

اندازه ی حروف، رنگ اونها، و محل قرارگیریشون فرق میکنه و این کار تشخیص حرف گمشده رو سخت میکنه پس باید دقت ، تمرکز و سرعت داشته باشید تا بتونید امتیاز لازم رو برای رفتن به مرحله بعد کسب کنید.

نويسنده : شایان محمودی | تاريخ : سه شنبه 18 مهر 1391برچسب:بازی ریاضی , بازی ریاضی , بازی ریاضی , بازی ریاضی,

| نوع مطلب : <-PostCategory-> |

مقدمه:
در دوره راهنمایی وقتی دانش آموزان با مفهوم جمع اعداد صحیح آشنا شدند و بدست آوردن حاصل جمع رو با نوشتن راه حل مربوطه(روش قرینه یابی و مختصرنویسی) یاد گرفتند لازم هست که روش بدست آوردن حاصل جمع اعداد صحیح بصورت ذهنی رو هم یاد بگیرند تا بعدها در قسمت جمع اعداد گویا بتوانند بعد از مخرج مشترک گرفتن از دو کسر ، برای ساده کردن عبارت صورت آن کسر استفاده کنند.

درباره بازی:
طراحی این بازی به منظور تقویت مهارت" پیدا کردن ذهنی حاصلجمع اعداد صحیح" در دانش آموزان دوره راهنمایی بوده است.
دانش آموز باید پاسخ هر جمع که از او خواسته شده را در بین دسته ای از گلها پیدا کند. بعضی مواقع برای پیدا کردن جواب در لابه لای گلها باید بگردد و بعد از پیدا کردن جواب روی آن دبل کلیک کند تا امتیاز مربوطه را کسب کند.

هر آزمون شامل 20 سئوال میشه و اگر دانش آموز پاسخ اشتباهی را انتخاب کند ،پاسخ صحیح به او نشان داده میشه.سئوالات بطور کاملاًتصادفی انتخاب میشوند و امکان حفظ کردن سئوالات نیست.
بازی در دو سطح معمولی و پیشرفته طراحی شده است که در سطح پیشرفته سه عدد صحیح با هم جمع میشوند.

برای جذاب تر شدن بازی از رنگهای متنوع و افکت های صوتی و موزیک استفاده شده است.

امیدوارم مورد توجه دانش آموزان و دبیران ریاضی مقطع راهنمایی قرار بگیره
اگر پیشنهاد ایده یا انتقادی راجع به بازی داشتید در قسمت نظرات مطرح بفرمایید.
برای دیدن بازی و یا دانلود آن (با حجم170کیلوبایت) روی تصویر بالا کلیک کنید.

نويسنده : شایان محمودی | تاريخ : سه شنبه 18 مهر 1391برچسب:یازی ریاضی بازی ریاضی بازی ریاضی,

| نوع مطلب : <-PostCategory-> |